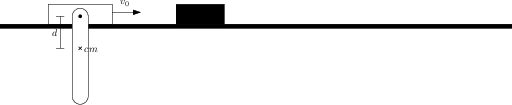Esercitazioni di Fisica 1
Ultima versione: \today
Urti con corpi rigidi
1 Urto di una particella contro un disco
Un disco di raggio
e massa
è appoggiato su un piano senza attrito, e si trova inizialmente in quiete. Una particella di massa
e velocità
lo colpisce sul bordo, con un parametro d’urto
. L’urto è completamente anelastico e istantaneo, e la particella rimane fissata sul bordo del disco.
Calcolare il momento di inerzia dell’unico corpo rigido finale, rispetto al suo centro di massa.
Il momento di inerzia del solo disco relativo al suo centro di massa è
. Il centro di massa del corpo rigido finale si troverà ad una distanza dal centro del disco data da
e utilizzando il teorema di Steiner troviamo il momento di inerzia cercato:
Descrivere il moto dopo l’urto.
Dopo l’urto abbiamo un unico corpo rigido: dato che non si hanno forze e momenti esterni il suo centro di massa avrà una velocità costante
, e il corpo ruoterà con velocità angolare
.
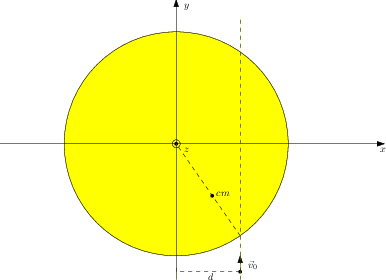
Per la stessa ragione durante l’urto si conserva il momento angolare e la quantità di moto totale. Utilizzando il sistema di coordinate in Figura 1↑ abbiamo per la quantità di moto
e quindi
Per il momento angolare invece, prendendo come polo il centro del disco
dove
è il vettore posizione del punto di impatto e
quello del centro di massa del sistema. Quindi
L’unica componente non nulla è quella lungo
, e si ha
ossia
Calcolare la velocità del centro del disco immediatamente dopo l’urto.
Dato che
abbiamo
Quindi la componente
della velocità è sempre negativa (o nulla), e quella
sempre positiva.
Trovare un eventuale punto fisso del corpo rigido dopo l’urto.
Detto
il vettore posizione dell’eventuale punto fisso, dovremo avere
Se
questa equazione si riduce a
. Questo è un caso banale: in assenza di rotazione tutti i punti del corpo sono fissi (se il corpo è fermo) oppure nessuno lo è.
Se invece
calcoliamo il prodotto vettore con
ottenendo
ma dato che
è perpendicolare a
possiamo anche scrivere
e quindi
Trovare quanta energia è persa nell’urto.
Possiamo calcolare direttamente la variazione di energia dai dati precedenti. Abbiamo
La minore perdita si ha per
,
Notare che la frazione dell’energia disponibile nel centro di massa che può essere dissipata è
che è uguale a
solo per
.
Possiamo guardare a questo risultato da un altro punto di vista. Sappiamo che l’energia totale del sistema si può scrivere, sia prima che dopo l’urto, nella forma
dove
è la velocità del centro del disco,
la sua velocità angolare e
la velocità della particella. Abbiamo in tutto
gradi di libertà. Possiamo però utilizzare una parametrizzazione alternativa, scegliendo
di questi
come quantità conservate, cioè le due componenti della quantità di moto totale
e il momento angolare totale rispetto al centro di massa del sistema (che sappiamo essere diretto sempre perpendicolarmente al piano)
dove
è il vettore posizione della particella,
quello del centro del disco e
quello del centro di massa
Restano due gradi di libertà, che sceglieremo nel modo seguente:
Chiaramente quando la particella è solidale al disco
.
Vediamo se è possibile scrivere l’energia totale in funzione di
,
e
. Sappiamo dal teorema di Koenig che è possibile porre
Dalle Equazioni (↓) e (↓) possiamo scrivere
e quindi
Questo è il risultato cercato: espandendo i quadrati otteniamo
L’ultimo termine calcolato immediatamente prima dell’urto deve corrispondere all’energia dissipata. Nel nostro caso
e
e quindi
e ponendo
\endcomment
2 Urto elastico di una particella contro una sbarra
Una sbarra di lunghezza
e massa
viene urtata elasticamente da una particella di massa
con velocità iniziale
. L’urto avviene in una posizione
rispetto al centro di massa, e la velocità
è perpendicolare alla sbarra.
Calcolare la velocità finale della particella, la velocità finale del centro di massa della sbarra e la velocità angolare finale della sbarra.
Oltre all’energia nell’urto si conserva la quantità di moto e il momento angolare del sistema. Esplicitamente la conservazione dell’energia si scrive
quella della quantità di moto
e quella del momento angolare (ponendo la sbarra sull’asse
di un sistema di coordinate Cartesiane con il centro di massa nell’origine)
Infine si conserva la quantità di moto della particella lungo
, dato che durante l’urto le forze impulsive che la sbarra applica ad essa sono lungo
. Di conseguenza
e
. Le equazioni precedenti si riducono dunque a
Ricaviamo
:
e sostituendo nell’energia troviamo
oppure, dividendo membro a membro,
Infine
e quindi
Calcolare le formule precedenti se l’urto avviene in un estremo della sbarra.
In questo caso
e quindi
Trovare un punto fisso per la sbarra.
Indicando con
la posizione del punto fisso rispetto al centro della sbarra abbiamo
e quindi deve essere
Il punto fisso ha quindi la stessa ascissa del centro di massa, e si trova dalla parte opposta rispetto ad esso rispetto al punto nel quale è avvenuta la collisione.
Dove si deve colpire la sbarra affinche il punto fisso coincida inizialmente con un estremo della sbarra? Disegnare qualitativamente il campo di velocità della sbarra nell’istante iniziale e dopo una rotazione di
.
3 Urto di un pendolo fisico contro un ostacolo
Un estremo di una sbarra sottile di lunghezza
è imperniato e libero di ruotare attorno ad un supporto mobile. Questo può muoversi su un piano orizzontale privo di attrito. La massa del supporto è trascurabile, mentre quella della sbarra vale in totale
ed è distribuita su di essa in modo non noto. Si conosce però la posizione del centro di massa della sbarra, che si trova ad una distanza
dall’estremo imperniato. Inoltre il momento di inerzia della sbarra rispetto ad un asse passante per il suo centro di massa vale
con
costante.
Se al supporto è applicata una forza orizzontale costante
, quale deve essere l’angolo che la sbarra forma con la direzione verticale per rimanere in equilibrio?
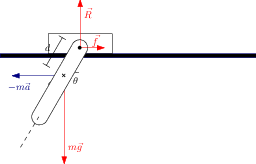
Le forze in gioco sono rappresentate in Figura 2↑. Prima di tutto osserviamo che se l’angolo
non varia l’accelerazione del sistema è data da
Consideriamo adesso diversi metodi di risoluzione.
Questo è un sistema di riferimento non inerziale, quindi avremo una forza apparente
applicata al centro di massa. Scegliendo il polo nel perno, avremo un momento totale dato da
che si annullerà quando
In questo caso la seconda equazione cardinale ci dice che
ma dato che il centro di massa non accelera in verticale
e troviamo nuovamente lo stesso risultato.
In questo caso la seconda equazione cardinale si scrive
ed anche se
il momento angolare del sistema cambia. Calcolando la derivata troviamo nuovamente
e quindi lo stesso risultato.
Supponiamo che il supporto si trovi inizialmente in moto con velocità costante
, e che la sbarra sia in posizione verticale in equilibrio stabile. Ad un certo momento il supporto incontra un ostacolo che lo blocca improvvisamente. Calcolare per quale valore minimo di
la sbarra compie un giro completo.
Facciamo riferimento alla Figura 3↑. Nell’urto si conserva il momento angolare rispetto al perno. Quindi
da cui la velocità angolare dopo l’urto
Da questo momento l’energia si conserva, e l’asta sarà in grado di compiere un giro completo se
cioè per
Nel caso precedente, quale relazione di deve essere tra
e
affinché l’energia si conservi nell’urto?
La variazione di energia nell’urto è
che si annulla se
. Questo significa che la massa della sbarra è tutta concentrata nel suo centro di massa, che si può trovare in una posizione arbitraria.