Esercitazioni di Fisica 1
G. Cella
Ultima versione: \today
Analisi dimensionale: concetti di base e semplici applicazioni.
1 Analisi dimensionale
Una legge fisica deve legare tra di loro in maniera quantitativa risultati di osservazioni sperimentali. Queste ultime si possono ricondurre a operazioni di confronto con riferimenti scelti in modo opportuno. Ad esempio, misurare una lunghezza (di un tavolo, di una strada etc.) significa confrontarla con una lunghezza di riferimento e il risultato della misura ci darà informazioni sul rapporto tra il riferimento (che chiameremo unità di misura) e quanto misurato.
Scrivendo
intenderemo dire che “la lunghezza
del tavolo misura
metri”, ossia il rapporto tra
e la lunghezza campione da noi scelta (in questo caso il metro [A] [A] La definizione di metro è cambiata nel tempo. Originariamente esso era posto uguale a
volte il meridiano terrestre. Successivamente divenne
volte la lunghezza d’onda della radiazione emessa in una particolare transizione atomica. Attualmente il metro è definito come lo spazio percorso dalla luce nel vuoto in
secondi., indicato dal simbolo m) è di
.
Le grandezze fisiche sono in generale quantità dimensionate, e sono espresse da una parte numerica (
nell’esempio precedente) e da una dimensione (
nell’esempio precedente).
Per poter esprimere le grandezze fisiche interessanti saranno quindi necessarie un certo numero di unità di misura. L’insieme di unità di misura scelte come riferimento costituiranno un sistema di unità di misura. Ad esempio nel cosiddetto sistema internazionale si scelgono le unità di misura di
Lunghezza: il metro (m): lo spazio percorso dalla luce nel vuoto in
secondi.
Tempo: il secondo (s): la durata di 9192631770 periodi della radiazione emessa in una particolare transizione del cesio 133
Massa: il kilogrammo (kg): la massa di un cilindro di una lega di platino e iridio custodito presso l’ufficio internazionale dei pesi e delle misure.
Temperatura: il grado Kelvin (K): la frazione
della temperatura termodinamica del punto triplo dell’acqua
ed altre ancora (ad esempio per l’intensità di corrente elettrica).
1.1 Unità derivate
Una volta definite le unità di misura fondamentali del nostro sistema, possiamo definire unità derivate. Ad esempio dalla definizione della velocità
segue che potremo esprimere il suo valore in un’unità data dal rapporto tra l’unità di misura della lunghezza e l’unità di misura del tempo. Nel sistema internazionale questo significa
(metri al secondo).
Chiediamoci adesso come cambia il valore numerico di una grandezza fisica se cambiamo il sistema di unità di misura. Per chiarezza prendiamo come riferimento il sistema internazionale, e definiamo delle nuove unità secondo la regola
dove
,
e
sono costanti numeriche. In questa trasformazione il valore numerico di una lunghezza verrà moltiplicato per
, il valore numerico di una massa per
, quello di un tempo per
. Indicheremo con
la dimensionalità della grandezza fisica
, ossia il fattore per il quale il suo valore numerico viene cambiato nella trasformazione precedente. Avremo così
e per una grandezza derivata come la velocità,
Per esempio la relazione tra sistema internazionale e sistema cgs è data da
e quindi
,
e
. Il valore numerico di una velocità cambierà quindi secondo la seguente regola:
Consideriamo adesso una determinata legge fisica. Essa potrà assumere ad esempio la forma di una uguaglianza tra due grandezze fisiche. Dato che non ci aspettiamo che tale uguaglianza debba dipendere dal sistema di unità di misura scelto, segue che le due grandezze fisiche uguagliate dovranno avere la stessa dimensione.
Consideriamo ad esempio una ipotetica legge della forma
che dovrebbe legare il periodo
di un pendolo all’accelerazione di gravità
. Si può certamente trovare un sistema di unità di misura [B] [B] Basta scegliere come unità di misura della lunghezza quella del pendolo considerato. nel quale la legge è verificata. Ma dato che
essa non sarà valida in generale in un sistema diverso. Quindi la richiesta di indipendenza delle leggi fisiche dal sistema di unità di misura pone dei vincoli sulla forma delle leggi fisiche.
Un altro esempio: l’affermazione “la massa di un batterio è molto piccola” ha senso fisico? La risposta è negativa. Potremmo cercare di formularla scrivendo
e la relazione precedente è certamente verificata nel sistema internazionale, dato che [C] [C] Abbiamo preso come riferimento l’Escherichia coli.
D’altra parte, se scegliamo come unità di misura la massa di un elettrone avremo
e quindi in questo caso
.
Possiamo parlare invece di grandezze fisiche molto piccole rispetto ad altre grandezze fisiche delle stesse dimensioni. Ad esempio l’affermazione “la massa di un batterio è molto maggiore di quella di un elettrone” ha perfettamente senso. Detto in altri termini, possiamo scrivere disuguaglianze del tipo (↓) solo per quantità adimensionali, ad esempio
Il fatto che non esiste un sistema di unità di misura privilegiato rispetto agli altri ha altre conseguenze. Ad esempio vale il seguente teorema: La dimensionalità di una grandezza fisica è sempre un monomio delle dimensioni fondamentali.
Per dimostrarlo consideriamo per semplicità sistemi di unità di misura aventi per dimensioni di base
,
e
. Allora le dimensioni di una grandezza fisica
saranno esprimibili nella forma
senza possibili dipendenze da altri parametri, dato che vogliamo trattare tutti i sistemi di unità di misura in modo equivalente. Consideriamo adesso un sistema di unità di misura di base, nel quale il valore numerico della grandezza considerata è
. In un altro sistema (legato al sistema di base dalle scale
,
e
) il valore numerico della stessa quantità sarà
e in un altro ancora (legato al sistema di base dalle scale
,
e
) avremo
Allora potremo scrivere
ma anche
da cui otteniamo che la funzione
deve avere la proprietà
Conviene prendere il logaritmo di ambo i membri. Poniamo
e quindi
Deriviamo rispetto a
:
e poniamo
,
e
, ottenendo
dove abbiamo introdotto la costante
definita da
L’equazione differenziale (↓) si risolve facilmente introducendo la variabile
. Essa diventa infatti
e quindi deve essere
Inseriamo questo risultato nella (↓) che diviene\strikeout off\uuline off\uwave off
\uuline default\uwave defaultossia
Questa equazione è analoga alla (↓): ripetiamo quindi la procedura derivando questa volta rispetto a
, per ottenere
dove
è una nuova costante. Sostituendo nella (↓) abbiamo adesso
e ripetendo la procedura derivando rispetto a
otteniamo infine
(
è una terza costante). Mettendo insieme i termini ottenuti abbiamo infine
e quindi
Una conseguenza interessante di questo fatto è che deve sempre essere possibile esprimere una legge fisica in una forma nella quale eventuali funzioni diverse dalla potenza abbiamo solo argomenti adimensionali. Non devono apparire ad esempio espressioni del tipo
e così via.
2 Il teorema di Buckingam
Vogliamo formalizzare in maniera chiara i vincoli posti dall’analisi dimensionale alla forma delle leggi fisiche. Preliminarmente diamo una definizione: diremo che delle grandezze fisiche
hanno dimensioni indipendenti tra di loro se non è possibile costruire con esse un monomio adimensionale
dove
e
sono costanti numeriche. Ad esempio massa, velocità e energia hanno dimensioni dipendenti perchè
e quindi
Se le dimensioni delle quantità considerate sono indipendenti, è sempre possibile trovare un nuovo sistema di unità di misura nel quale il valore numerico di una di esse è moltiplicato per un fattore arbitrario, e i valori numerici delle altre restano invariati (per una dimostrazione vedere [1], Capitolo 1).
Supponiamo adesso di sapere che una data legge fisica deve essere esprimibile nella forma
dove
,
e
sono grandezze fisiche e
una funzione ignota. Abbiamo scelto le
quantità
in modo tale che le
rimanenti
abbiano una dimensione da esse dipendenti, ossia
per opportune costanti
.
Segue che deve anche essere
altrimenti per quanto detto precedentemente sarebbe possibile scegliere un nuovo sistema di unità di misura nel quale
varia di un fattore arbitrario mentre sia le quantità
che le
restano invariate. La legge fisica quindi non potrebbe essere valida in qualsiasi sistema.
Introduciamo adesso le combinazioni adimensionali
utilizzando le quali possiamo riesprimere la legge (↓) nella forma
Adesso possiamo arrivare alla conclusione che ci interessa: dato che le quantità
,
sono adimensionali, il loro valore non cambia se scegliamo nuove unità di misura. Al tempo stesso, è possibile scegliere unità di misura in modo che una delle
cambi per un certo fattore, e tutte le altre restino invariate. Di conseguenza la nuova funzione
non può dipendere veramente dagli
, e potremo scrivere
oppure, più esplicitamente,
Questo è il cosiddetto teorema
(o teorema di Buckingam). Una legge fisica per una quantità dimensionata
, dipendente da un certo numero di parametri dimensionati
e
, si può scrivere come prodotto di un fattore della stessa dimensione di
costruito con i parametri moltiplicato per una funzione arbitraria di tutte le combinazioni adimensionali indipendenti dei parametri stessi.
La definizione di parametri adimensionali indipendenti è la seguente: non deve essere possibile esprimere uno di essi come monomio degli altri.
3 Semplici applicazioni dell’analisi dimensionale
Un corpo di massa
viene lasciato cadere da un’altezza
. Cosa si può dire sul tempo di caduta, sulla base della sola analisi dimensionale?
I parametri in gioco sono
,
e l’accelerazione di gravità
. Le relative dimensioni sono
Consideriamo le combinazioni dei parametri del tipo
con le dimensioni di un tempo. Deve essere
da cui si ottengono le condizioni
che sono soddisfatte solo per
,
,
. Il tempo di caduta sarà quindi dato da
dove
è una costante numerica adimensionale, non calcolabile sulla base della sola analisi dimensionale. Usando la legge del moto accelerato
si conferma il risultato ottenuto, e si trova
.
Lo stesso corpo di massa
viene lanciato verso l’alto con velocità
. Cosa si può dire sull’altezza massima raggiunta, sulla base dell’analisi dimensionale?
I parametri in gioco sono
,
e
. Dobbiamo costruire con essi una grandezza con le dimensioni di una lunghezza. Quindi
e l’unica possibile soluzione è
,
e
, che corrisponde a
Analizzare dimensionalmente il problema del periodo di oscillazione di un pendolo inizialmente inclinato di un angolo
.
I parametri in gioco sono la massa del pendolo
, la sua lunghezza
, l’accelerazione di gravità
e l’inclinazione iniziale
. Vogliamo con essi costruire una grandezza delle dimensioni di un tempo, cioè
Il sistema precedente fissa
,
. Il parametro
può essere scelto arbitrariamente: questo corrisponde al fatto che
è adimensionale. La soluzione per il periodo sarà quindi della forma
dove
è una funzione arbitraria dell’angolo iniziale. Questa funzione esprime una possibile dipendenza (che in effetti esiste) del periodo di oscillazione di un pendolo dalla sua ampiezza. Il principio di isocronia delle oscillazioni, valido approssimativamente per piccole ampiezze, ci dice che
dove
è una costante strettamente maggiore di zero. Risolvendo le equazioni del moto si trova che la formula è corretta, e che
.
Dimostrare il teorema di Pitagora usando l’analisi dimensionale.
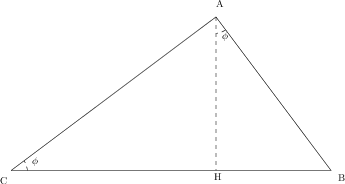
Consideriamo il triangolo rettangolo in Figura 1↓. L’area della sua superficie dipenderà univocamente dalla lunghezza dell’ipotenusa
e dall’angolo
. Allora sulla base di considerazioni dimensionali potremo scrivere
Dove
è una funzione incognita.
Consideriamo adesso il triangolo rettangolo
. Per la stessa ragione l’area della sua superficie sarà
e per il triangolo
Dato che
avremo, utilizzando quanto appena ottenuto,
ossia, una volta semplificato il fattore comune, il risultato cercato.