Esercitazioni di Fisica 1

G. Cella

Ultima versione: \today

1 Automobili e api

Figure 1 Rappresentazione grafica del moto delle due automobili, nei casi $V_{1}>V_{2}$ e $V_{1}<V_{2}$ .

2 Semafori

1. si è già fermato, prima dell’incrocio: $$\tau>t_{*}\,\bigcap\, s\left(t_{*}\right)<d$$
2. si è già fermato, oltre l’incrocio: $$\tau>t_{*}\,\bigcap\, s\left(t_{*}\right)>d+h$$
3. non si è ancora fermato, ma è già oltre l’incrocio: $$\tau<t_{*}\,\bigcap\, s\left(\tau\right)>d+h$$
4. non si è ancora fermato, ma riuscirà a fermarsi prima dell’incrocio: $$\tau<t_{*}\,\bigcap\, s\left(\tau\right)<d$$

1. si è già fermato, prima dell’incrocio: $$\tau>\frac{v_{0}}{a}\,\bigcap\,\frac{v_{0}^{2}}{2a}<d$$
2. si è già fermato, oltre l’incrocio: $$\tau>\frac{v_{0}}{a}\,\bigcap\,\frac{v_{0}^{2}}{2a}>d+h$$
3. non si è ancora fermato, ma è già oltre l’incrocio: $$\tau<\frac{v_{0}}{a}\,\bigcap\, v_{0}\tau-\frac{1}{2}a\tau^{2}>d+h$$
4. non si è ancora fermato, ma riuscirà a fermarsi prima dell’incrocio: $$\tau<\frac{v_{0}}{a}\,\bigcap\, v_{0}\tau-\frac{1}{2}a\tau^{2}<d$$

1. si è già fermato, prima dell’incrocio: $$\left(\Pi_{2}>\frac{1}{2}\right)\,\bigcap\,\left(\Pi_{1}<4\Pi_{2}\right)$$
2. si è già fermato, oltre l’incrocio: $$\left(\Pi_{2}>\frac{1}{2}\right)\,\bigcap\,\left[\Pi_{1}>4\Pi_{2}\left(1+\Pi_{3}\right)\right]$$
3. non si è ancora fermato, ma è già oltre l’incrocio: $$\left(\Pi_{2}<\frac{1}{2}\right)\,\bigcap\,\left[\Pi_{1}\left(1-\Pi_{2}\right)>1+\Pi_{3}\right]$$
4. non si è ancora fermato, ma riuscirà a fermarsi prima dell’incrocio: $$\left(\Pi_{2}<\frac{1}{2}\right)\,\bigcap\,\left[\Pi_{1}\left(1-\Pi_{2}\right)<1\right]$$

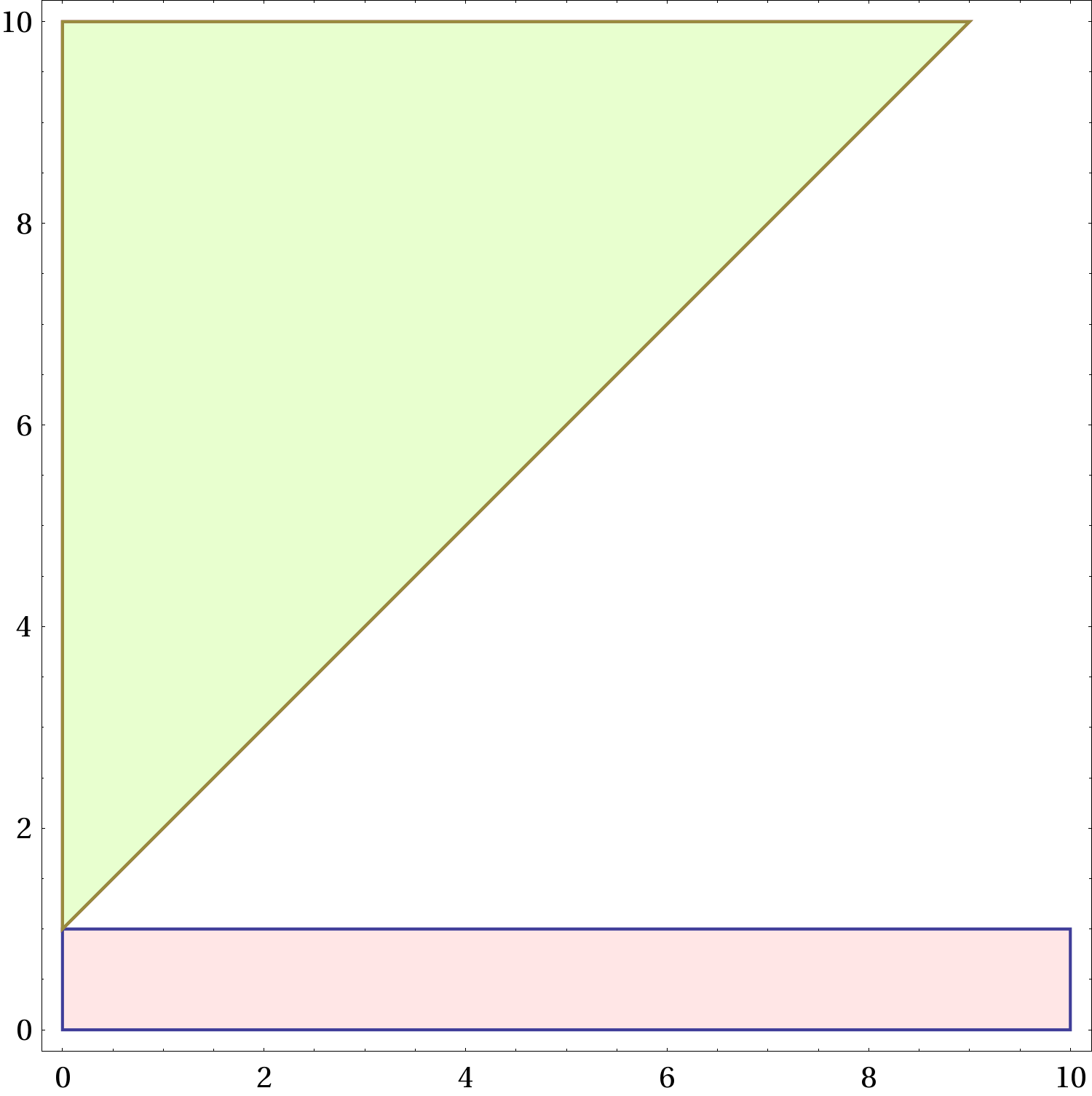
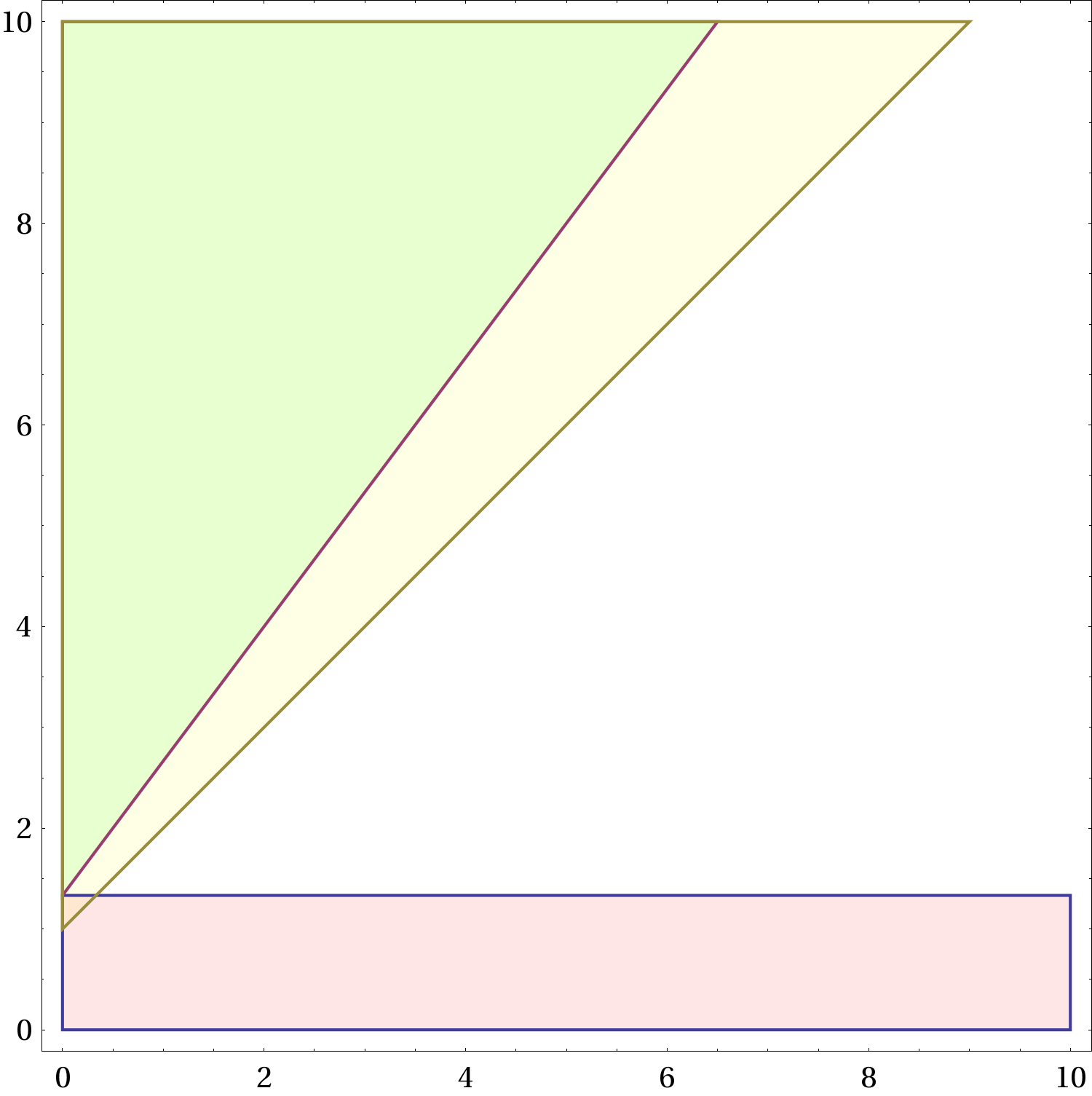
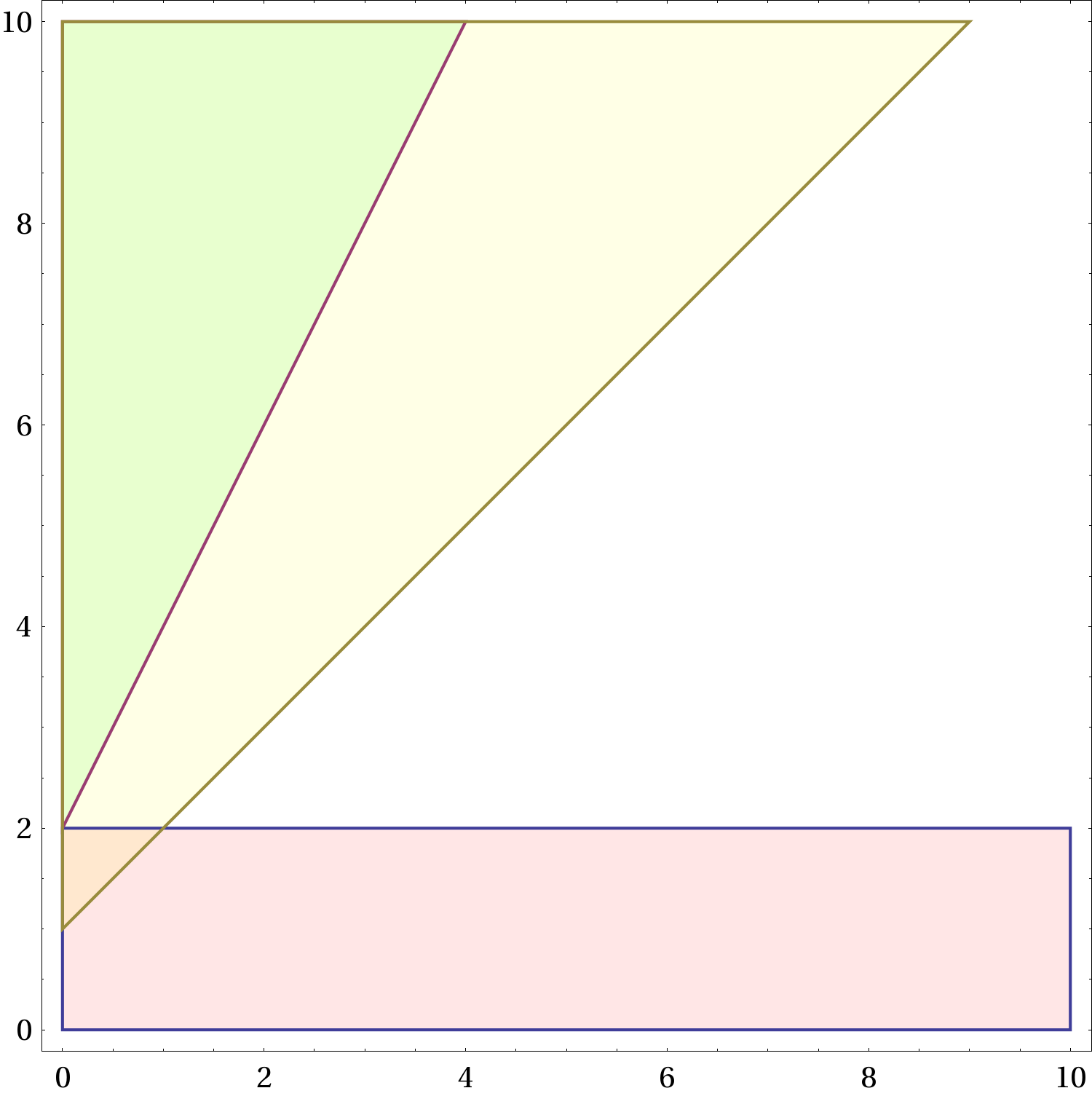
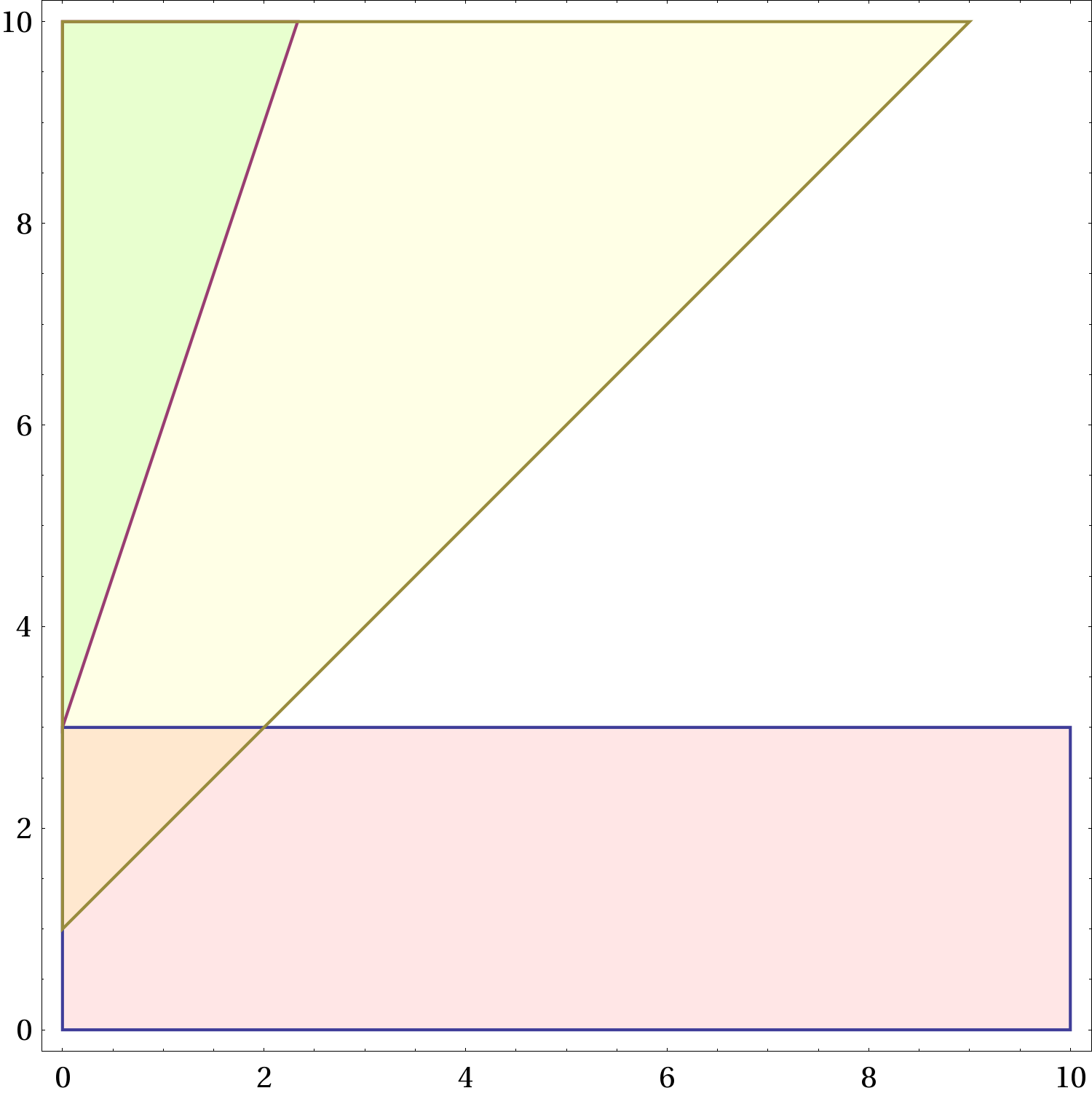
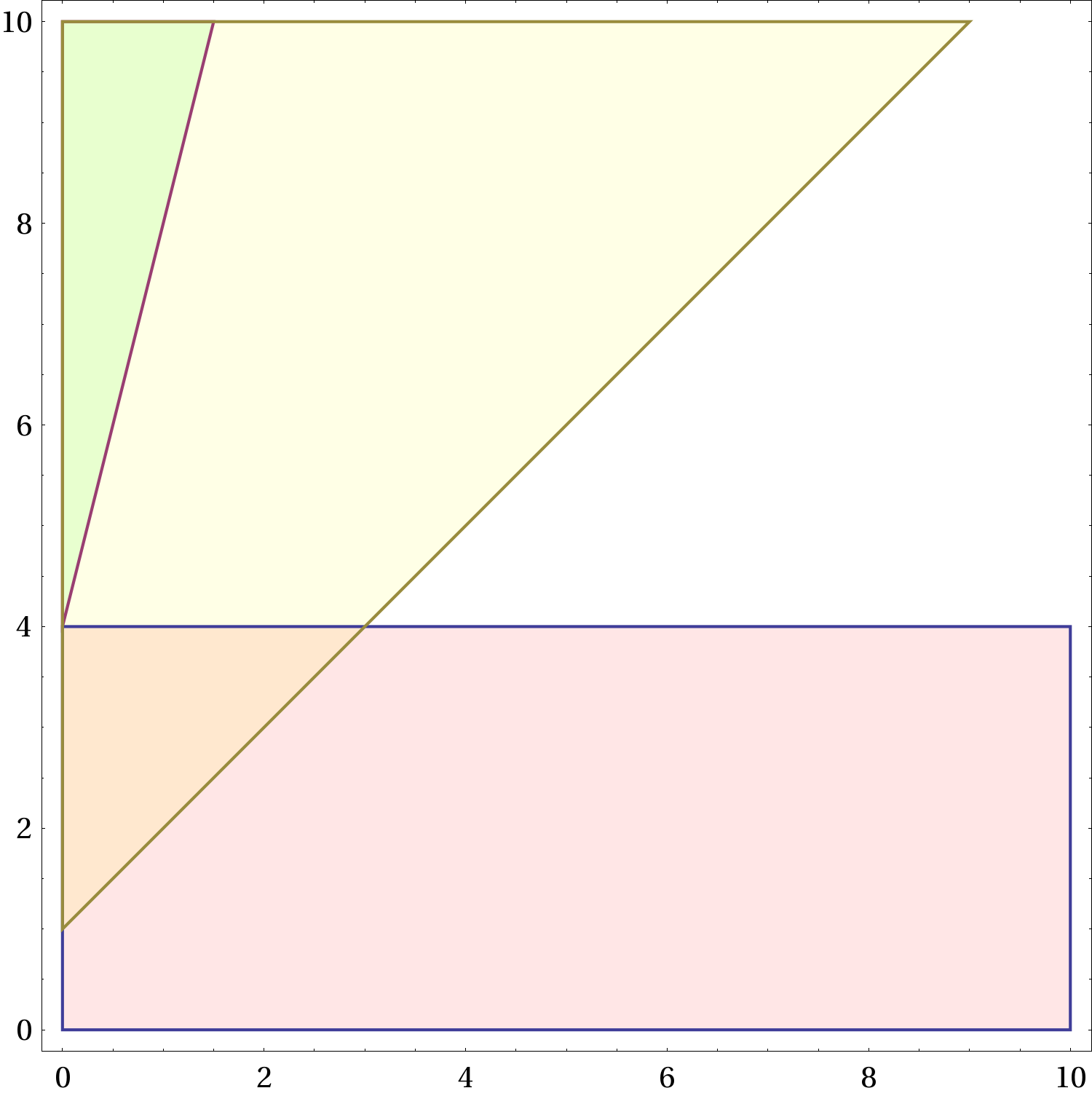
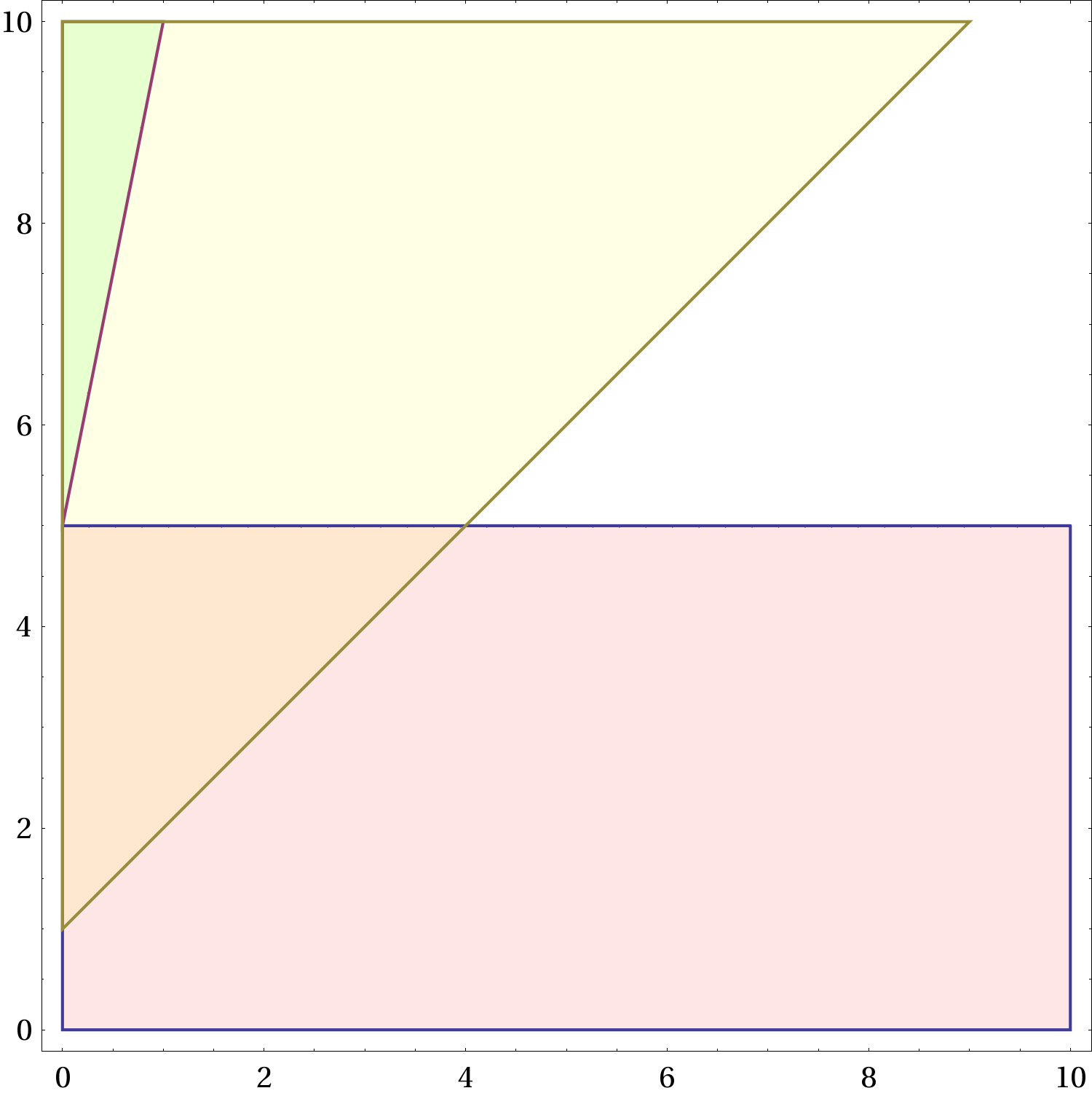
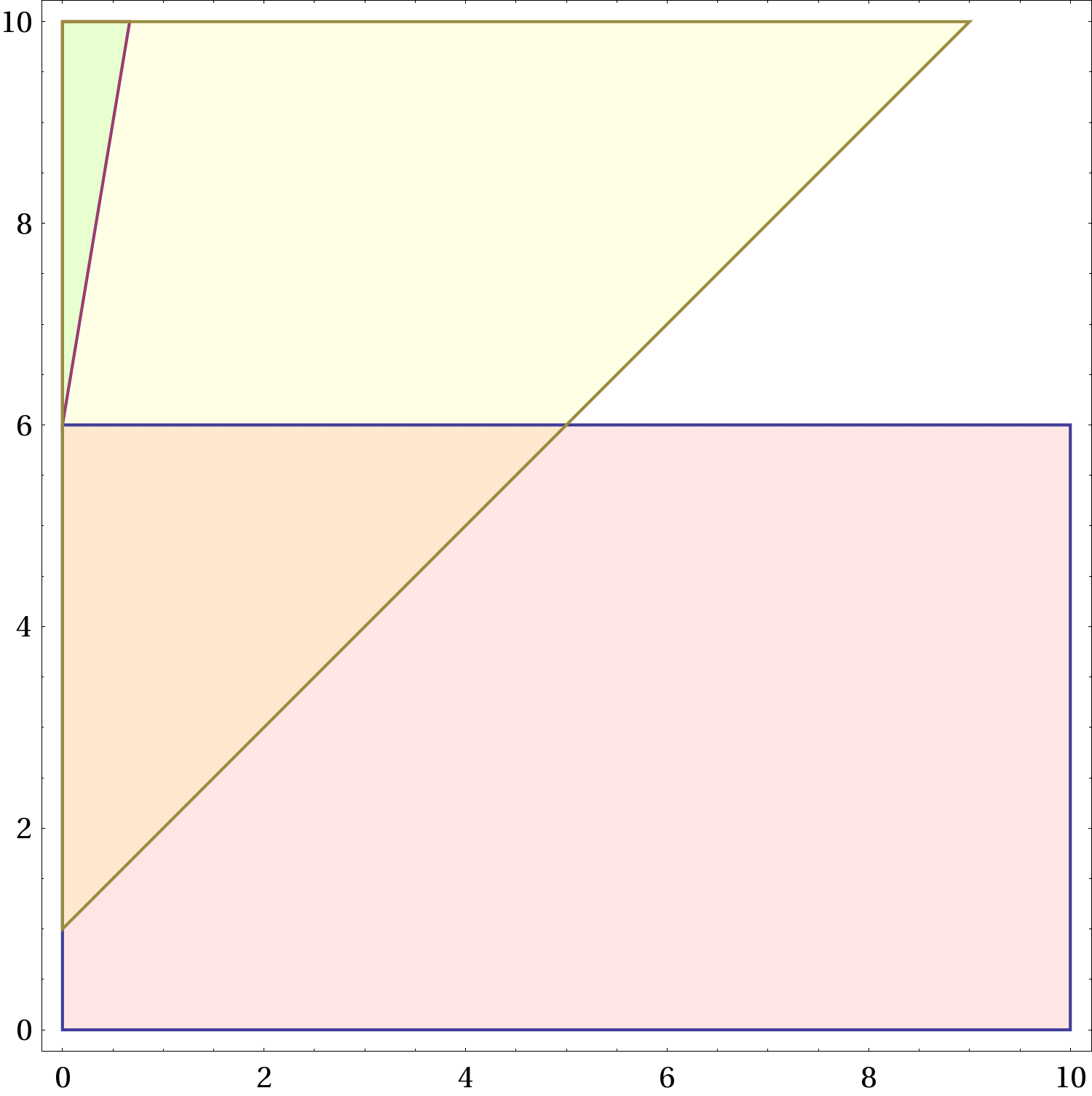
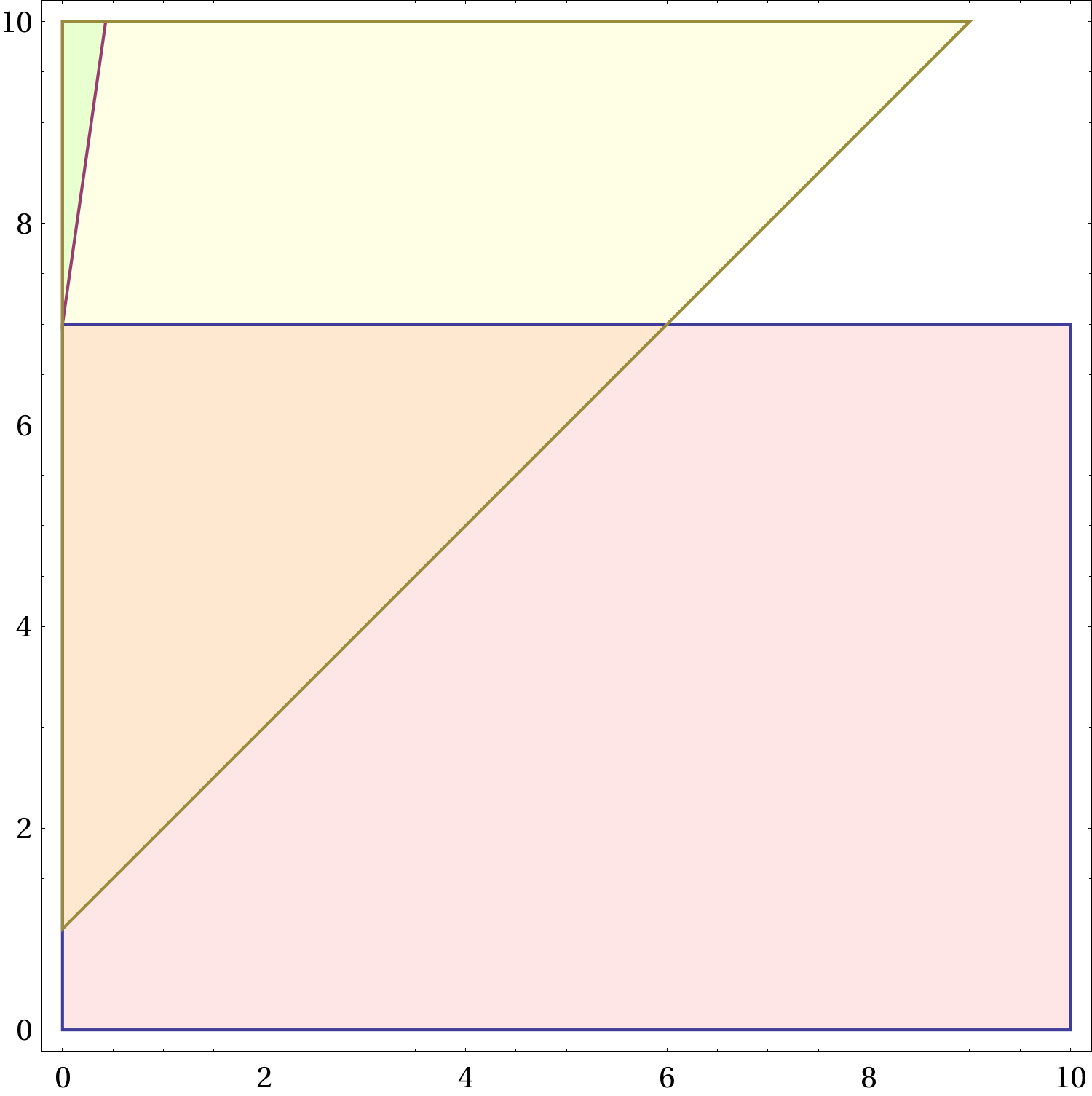
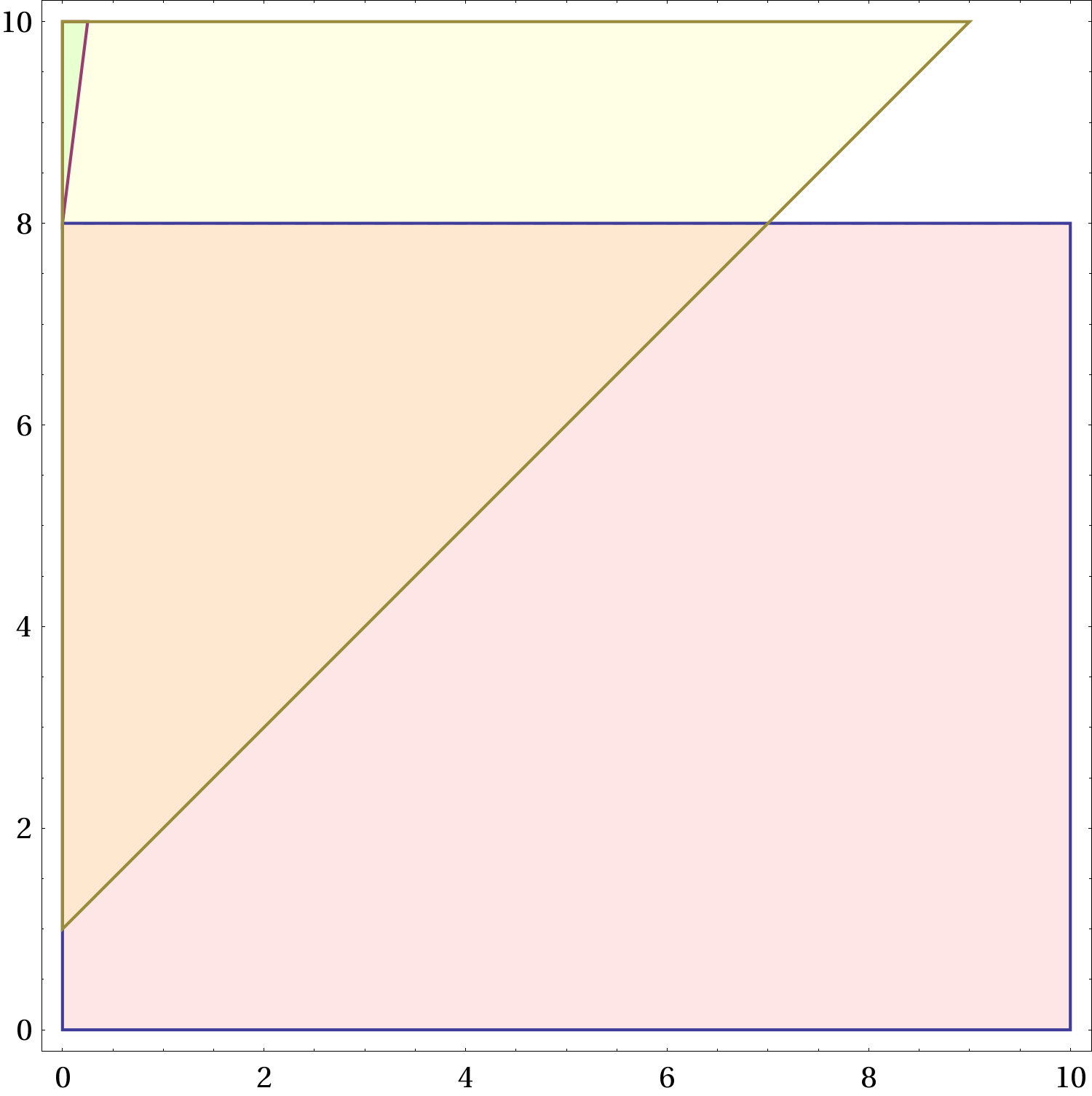
Figure 2 Le regioni ammesse nel piano $\Pi_{3},\Pi_{2}$ ($\Pi_{3}$ è l’asse verticale, $\Pi_{1}$ quello orizzontale) al variare di $\Pi_{2}$ . Partendo dall’alto verso il basso e da sinistra a destra $\Pi_{2}=0,1/4,1/2,3/4,1,5/4,3/2,7/4,2$ . La regione gialla, che non dipende da $\Pi_{2}$ e quindi è la stessa in tutte le figure, corrisponde alle combinazioni dei parametri per i quali è possibile non frenare. La regione rossa corrisponde a una frenata che porta a fermarsi prima del semaforo. Quella azzurra corrisponde a una frenata che porta a fermarsi oltre il semaforo, senza rimanere in mezzo. All’aumentare di $\Pi_{2}$ (frenata “forte”) la regione rossa aumenta, quella azzurra si restringe. Il verde indica una sovrapposizione di regione azzurra e regione gialla, l’arancio una sovrapposizione di regione gialla e regione rossa.

Alcuni grafici sono riportati in Figura 2↑. Nella zona solo gialla (non ricoperta dall’area verde) l’unica scelta possibile è non frenare. Nella zona rossa l’unica scelta possibile è frenare. Infine nella regione arancio o verde sono possibili entrambe le alternative.

3 Profondità di un pozzo