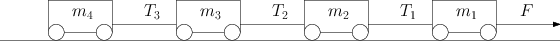Esercitazioni di Fisica 1
G. Cella
Ultima versione: \today
Piani inclinati e carrucole.
1 Un treno
Consideriamo per iniziare un treno con un certo numero di vagoni (ad esempio
) collegati tra di loro da dei cavi inestensibili e di massa trascurabile. Il primo vagone è trainato da una forza costante
. Vogliamo determinare l’accelerazione dei vagoni e la tensione dei diversi cavi.
Osserviamo prima di tutto che lo spazio percorso da ciascun vagone in un dato intervallo di tempo è lo stesso. Segue che tutti i vagoni hanno la stessa velocità e la stessa accelerazione. Chiameremo quest’ultima
.
Scriviamo adesso le equazioni del moto per i vagoni. Le forze orizzontali che agiscono sul primo sono la forza esterna
e la forza
dovuta al cavo. Di conseguenza
I vagoni intermedi risentono della forza dei due cavi ad essi collegati, quindi
Infine l’ultimo vagone è collegato ad un solo cavo, e quindi
Se sommiamo membro a membro tutte le equazioni otteniamo
e quindi possiamo determinare l’accelerazione,
La prima equazione da adesso
Sommando la prima e la seconda otteniamo
sommando le prime tre infine
Vediamo che le tensioni decrescono verso la coda del treno.
Nel risolvere il problema abbiamo implicitamente assunto che, quando un cavo è sottoposto ad una tensione
, esercita una forza di trazione di uguale modulo su un corpo a cui è attaccato.
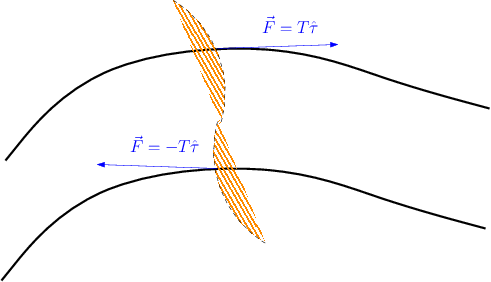
Figure 2 Due esempi di un filo sotto tensione separato in due parti da una superficie. In entrambi i casi la separazione avviene in un punto nel quale la tensione è
. Abbiamo indicato con una tratteggio la parte che consideriamo “interna” alla superficie. In entrambi i casi abbiamo rappresentato la forza applicata alla parte “interna”.
Cerchiamo di dare una definizione più precisa: supponiamo che la tensione di un cavo in un suo punto sia
. Separiamo il cavo in due parti in tale punto con una superficie orientata (cioè, con una convenzione sulla parte che consideriamo “esterna” e quella che consideriamo “interna”). Allora la parte esterna eserciterà una forza su quella interna di modulo
, direzione tangente al filo e verso “uscente” (vedere Figura 2↑).
Questa definizione è consistente con il terzo principio: infatti la forza che la parte “esterna” esercita su quella “interna” è uguale e opposta a quella che la parte “interna” esercita su quella “esterna”.
In realtà abbiamo fatto un’altra assunzione: la tensione di ogni filo è costante. Nel caso preso in considerazione questo si capisce facilmente. Supponiamo ad esempio che la tensione del primo cavo valga
nel punto di attacco con il primo vagone, e
nel punto di attacco con il secondo. Deve allora valere
dove
è la massa del filo. Ma dato che questa è trascurabile sarà
.
2 Una paranco
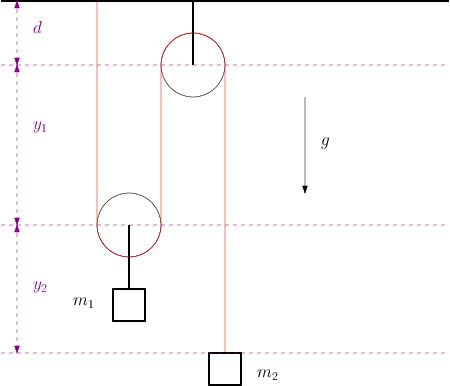
Vogliamo studiare adesso il sistema rappresentato in Figura 3↓. Abbiamo due masse
ed
collegate tra di loro da un filo inestensibile e di massa trascurabile.
Il filo si avvolge attorno a due cilindri fissi (anche essi di massa trascurabile) e privi di attrito. Vogliamo calcolare l’accelerazione delle due masse, e la tensione del filo. Assumeremo che quest’ultima sia la stessa ovunque: in seguito daremo una giustificazione generale per questo.
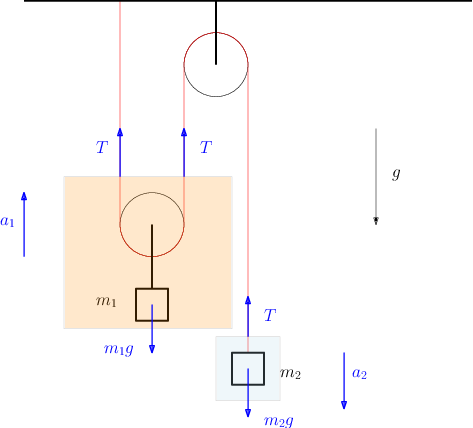
Consideriamo quindi le equazioni del moto per le due parti del sistema rappresentate in Figura 4↑. Considereremo l’accelerazione
della parte indicata dal box arancio come positiva se diretta verso l’alto. L’accelerazione
della parte indicata dal box azzurro sarà invece positiva se diretta verso il basso.
Le equazioni del moto per le due parti saranno dunque
Vediamo subito che abbiamo tre incognite (
,
e
) ma due sole equazioni. \’E dunque necessario trovare un’altra relazione.
Osserviamo che non abbiamo ancora utilizzato la inestensibilità del filo: questo ci darà un legame tra le due accelerazioni. Per trovarlo torniamo alla Figura 3↑. Vediamo che possiamo scrivere la lunghezza totale del filo come
dove
e
sono i raggi delle due carrucole, che come vedremo non giocano alcun ruolo. Derivando due volte ambo i membri di questa equazione rispetto al tempo troviamo
Osserviamo adesso che
da cui
Adesso abbiamo un numero di equazioni sufficiente. Utilizzando la (↓) possiamo riscrivere le (↓) eliminando
e sommando membro a membro alla prima equazione il doppio della seconda troviamo
A questo punto è facile trovare l’accelerazione
e la tensione del filo
Possiamo chiederci in quali condizioni il sistema si può trovare all’equilibrio. Dato che in questo caso le accelerazioni sono nulle, abbiamo
e questo significa che il sistema si può utilizzare per sollevare una massa
applicando una forza
, la metà di quella che sarebbe necessaria per sollevarla direttamente. Notiamo infine che in queste condizioni la tensione del filo vale
come ci si poteva aspettare osservando che la somma delle forze applicate a
deve essere zero.
2.1 Perchè la tensione lungo il filo è costante?
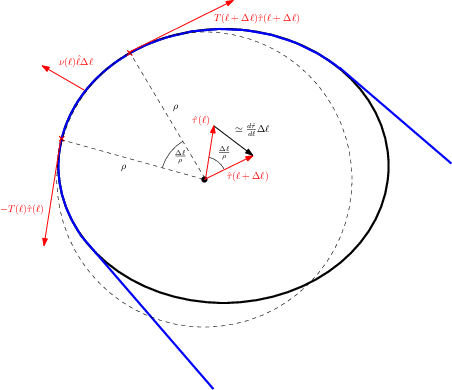
Cercheremo adesso di giustificare l’assunzione che abbiamo fatto, cioè che la tensione sia costante su tutto il filo. Per farlo consideriamo la situazione in Figura 5↓. Abbiamo un filo (rappresentato in colore blu) che si avvolge attorno ad un supporto, non necessariamente circolare.
Per identificare un punto appartenente al filo utilizzeremo la lunghezza
del tratto che lo separa da un punto particolare scelto come riferimento. Scriviamo adesso l’equazione del moto per un piccolo tratto compreso tra
e
. Abbiamo
dove
- è la massa per unità di lunghezza del filo. Quindi è la massa totale del tratto di filo considerato;
- è l’accelerazione del tratto di filo;
- è la forza applicata al tratto considerato dalla parte di filo oltre ;
- è la forza applicata al tratto considerato dalla parte di filo precedente
- è la reazione normale del supporto sul tratto considerato;
- è un’eventuale forza di attrito, tangente al supporto.
Dividiamo membro a membro per
, ottenendo
e passando al limite
otteniamo
Se separiamo la parte tangenziale e la parte normale dell’accelerazione, e calcoliamo la derivata al secondo membro, otteniamo
Per quanto riguarda la derivata del versore tangente, osserviamo che deve essere diretta come il versore normale. Infatti
Possiamo anche considerare la costruzione al centro in Figura 5↑: vediamo che nel limite di piccoli
è un vettore diretto lungo
, di modulo
. Di conseguenza possiamo scrivere
e l’equazione generale diviene
Separando le componenti dirette lungo
e quelle dirette lungo
troviamo infine
e
Nel caso particolare che stiamo esaminando il filo è privo di massa (
) e non ci sono attriti (
). Di conseguenza l’Equazione (↓) diviene
cioè la tensione è costante. Notare che affinchè questa conclusione sia vera è necessario e suffuciente che
- non vi siano attriti;
- il filo abbia massa trascurabile, oppure non stia accelerando.
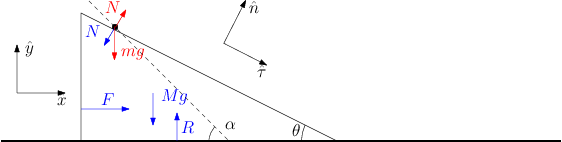
3 Piani inclinati
Consideriamo il piano inclinato di massa
in Figura 6↓.
Esso si trova appoggiato su un piano orizzontale privo di attrito sul quale è libero di scorrere. Al di sopra di esso si trova un punto materiale di massa
, anche esso libero di scorrere. Inoltre al piano è applicata una forza esterna orizzontale
. Considereremo negli esercizi che seguono tre diverse situazioni.
In questo caso vogliamo trovare il valore della forza esterna
che è necessario applicare per fare in modo che il piano non si muova. Possiamo scrivere anzitutto l’equazione del moto per questo nella direzione orizzontale, ottenendo
dove
è la forza di contatto normale applicata al piano dal punto materiale. Osserviamo adesso che il punto materiale non accelera nella direzione normale al piano, quindi deve essere
ed in conclusione
Notiamo che
si annulla per
(piano orizzontale) e per
(piano verticale). Nel primo caso il sistema è in equilibrio in assenza di forze esterne, nel secondo il punto materiale cade verticalmente senza applicare alcuna forza al piano inclinato. \qed
In questo caso vogliamo fare in modo che il punto materiale non scenda lungo il piano. Per fare questo sarà necessario far accelerare quest’ultimo: indicheremo con
questa accelerazione.
Scriviamo ancora una volta l’equazione del moto per il piano in direzione orizzontale. Abbiamo
Osserviamo adesso che l’accelerazione del punto materiale è la stessa del piano: di modulo
e orizzontale. Se consideriamo quindi l’equazione del moto per il punto nella direzione normale al piano abbiamo
Abbiamo tre incognite (
,
e
), ci serve quindi un’altra equazione. Possiamo considerare l’equazione del moto per il punto materiale nella direzione parallela al piano,
Otteniamo
Notare che vale
, e potevamo predire questo sin dall’inizio: il blocco e il punto materiale si possono infatti considerare come un’unica massa
.\qed
In questo caso porremo
e studieremo il moto del piano e del punto materiale. L’equazione per il moto orizzontale del piano non è diversa da quella dell’esercizio precedente (salvo che
)
Consideriamo adesso l’equazione del moto per il punto materiale nella direzione normale al piano. In tale direzione l’accelerazione del punto è la stessa del piano, e quindi come prima
Consideriamo adesso il moto del punto materiale nella direzione parallela al piano. In questo caso non c’è alcuna relazione tra l’accelerazione del piano e quella del punto materiale, che chiameremo
. Avremo
In conclusione
Calcoliamo adesso le componenti
e
dell’accelerazione del punto materiale. Abbiamo
L’accelerazione del punto materiale è dunque costante. Di conseguenza se questo è inizialmente fermo la sua traiettoria sarà rettilinea. Calcoliamo l’angolo tra la traiettoria e la direzione orizzontale (indicato con
nella Figura 6↑). Abbiamo
e vediamo che
. Terminiamo considerando due casi limite particolari.
Se
ci aspettiamo che il piano inclinato non si muova. In effetti abbiamo
e
che sono le usuali formula per un piano inclinato fisso.
Se
otteniamo invece
e
In questo caso il punto materiale cade verticalmente con accelerazione
, senza essere influenzato dal piano inclinato. Quest’ultimo deve accelerare in modo da “fare spazio”.