Esercitazioni di Fisica 1
Ultima versione: \today
Paracadutista (attrito viscoso). Filo con massa che pende da un tavolo.
1 Studio del moto di un paracadutista
Vogliamo studiare il moto di un paracadutista, utilizzando un modello semplificato. In particolare, immagineremo che l’effetto del paracadute possa essere rappresentato da una forza di attrito viscoso della forma
dove
è la velocità del paracadutista e
una costante positiva che tiene conto delle caratteristiche del mezzo e della forma del paracadute. Va sottolineato che si tratta di un modello molto semplificato, valido solo per velocità sufficientemente “piccole”, cioè se
dove
è una dimensione caratteristica del sistema e
una costante di opportune dimensioni (detta viscosità cinematica) che caratterizza il mezzo. Per l’aria a temperatura ambiente ad esempio
e quindi, prendendo
vediamo che deve essere
che è sicuramente non verificata per un paracadutista. In un modello più realistico la forza è proporzionale al quadrato della velocità.
Per iniziare a comprendere il significato dell’Equazione (↓) riscriviamola nella forma
e rappresentiamola nel piano avente per ascissa
e per ordinata
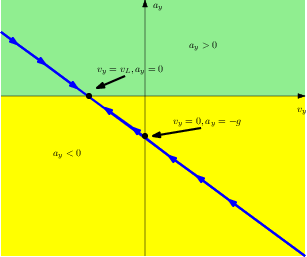
. Si tratta ovviamente di una relazione lineare, e il relativo grafico è in Figura (2↓). Possiamo estrarre delle informazioni utili facendo le seguenti considerazioni:
- se conosciamo la velocità del paracadutista ad un istante dato (ad esempio all’istante iniziale) il grafico ci permette di calcolare la accelerazione;
- se l’accelerazione è positiva la velocità successivamente aumenterà, diminuirà in caso contrario. Questo significa che se ad una data velocità ci troviamo sulla semiretta che giace nel semipiano , successivamente ci sposteremo su di essa verso destra. Se invece ci troviamo sulla semiretta che giace nel semipiano successivamente ci sposteremo verso sinistra.
Indipendentemente dalla velocità iniziale vediamo che le velocità convergeranno verso il valore corrispondente all’intersezione della retta con l’asse
, cioè
ed in particolare se inizialmente
sarà
, quindi tale velocità rimarrà costante.
Dal grafico che abbiamo costruito non possiamo però capire se la velocità convergerà alla velocità limite in un tempo finito. Proviamo allora a considerare il piano con ascissa
e ordinata
, come in Figura (3↓). Su di esso vorremmo cercare di rappresentare
.
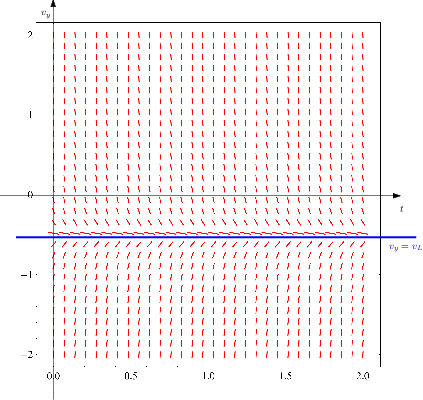
Figure 3 Una rappresentazione dell’Equazione (↓) nel piano
(in
)-
(in
). In ogni punto del piano l’equazione definisce la pendenza della curva. La retta orizzontale blu corrisponde a
: nei punti che le appartengono la pendenza è nulla. Si è scelto
.
Supponiamo di conoscere la velocità
a un dato tempo
,
. Possiamo dire con sicurezza che la curva
passerà dal punto
,
. Ma se scriviamo l’Equazione (↓) nella forma
vediamo che in realtà conosciamo anche la pendenza della curva in quel punto. In altre parole abbiamo la situazione rappresentata in Figura 3↑. Chiaramente la pendenza è negativa se
, positiva se
e nulla se
.
La legge
cercata corrisponderà a una curva che in ogni punto ha la giusta pendenza: nella Figura (4↓) sono rappresentate alcune di esse: è chiaro che per definire completamente quella che ci interessa dovremo dare altre informazioni, ad esempio il valore iniziale di
.
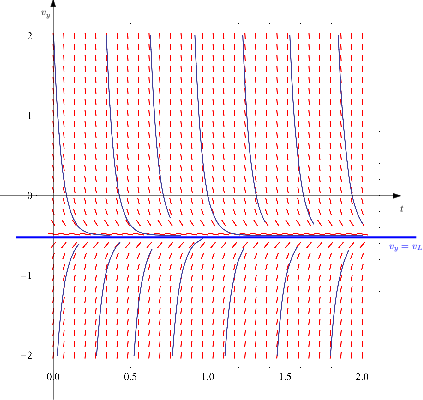
Figure 4 Una rappresentazione dell’Equazione (↓) nel piano
(in
)-
(in
). In ogni punto del piano l’equazione definisce la pendenza della curva. La retta orizzontale blu corrisponde a
: nei punti che le appartengono la pendenza è nulla. Si è scelto
. Sono state aggiunte delle possibili curve che in ogni punto hanno la giusta pendenza.
Consideriamo l’equazione approssimata
dove si è sostituito l’accelerazione istantanea con l’accelerazione media su un intervallo
. Si vuole cercare una soluzione per
.
Notiamo anzitutto che possiamo riscrivere la precedente nella forma
dove
. Risolvendo rispetto a
otteniamo
Questa è una relazione che dato il valore di
al tempo
ci permette di calcolarlo al tempo
. Iniziando da
abbiamo (dimostratelo, per esempio per induzione)
Poniamo adesso
e troviamo
dove
Esprimendo nuovamente tutto questo in funzione di
otteniamo
di conseguenza vediamo che
tende esponenzialmente alla velocità limite, indipendentemente dalle condizioni iniziali. \qed
Cerchiamo adesso di “indovinare” una soluzione dell’equazione esatta. Una semplice ipotesi è che anche in questo caso si tratti di qualcosa del tipo
dove
,
e
sono costanti da determinare. Derivando troviamo
e sostituendo nella (↓) troviamo
Raccogliendo i termini troviamo
Dato che il membro sinistro deve annullarsi per qualsiasi
, è necessario che i due termini si azzerino separatamente. Il secondo lo farà scegliendo
Il primo si annulla sicuramente per
: questo corrisponde alla soluzione a velocità costante
. Se
dovrà invece essere
e quindi la soluzione esatta sarà
ma dato che deve essere
possiamo anche scrivere
Se confrontiamo questa soluzione esatta con quella approssimata (↓) vediamo che l’unica differenza è nel coefficiente del termine esponenziale. Inoltre, come ci si può aspettare,
2 Filo con massa che pende da un tavolo
Consideriamo il sistema in Figura 5↓: un filo inestensibile di massa
e lunghezza
è parzialmente appoggiato su un piano orizzontale.
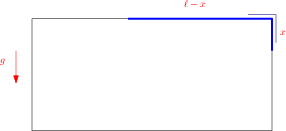
Figure 5 Il filo (in blu) considerato nel problema. \’E inestensibile, di lunghezza totale
e massa totale
, distribuita uniformemente. Nel disegno è stato aggiunto un vincolo aggiuntivo a forma di L attorno all’angolo superiore destro, per sottolineare che il filo è vincolato a non distaccarsi dal piano, cosa che farebbe se fosse semplicemente appoggiato.
Un tratto di lunghezza
pende inizialmente in verticale. Vogliamo capire come si muove il filo negli istanti successivi, in assenza di attrito, in presenza di un campo gravitazionale.
Scriviamo l’equazione del moto per il tratto di filo appoggiato sul piano orizzontale. Detta
la densità lineare di massa avremo
dove
è la tensione nel punto in cui il filo si piega. Per quanto riguarda il tratto di filo che pende verticalmente avremo invece
Sommando membro a membro troviamo
ossia
Supponiamo che sia
. La quantità
è costante nel tempo?
è il modulo della quantità di moto totale del sistema?
No. Infatti la quantità di moto totale si scrive
che in modulo vale
\qed
La quantità di moto totale del sistema si conserva se
?
Calcoliamo la derivata temporale della quantità di moto: abbiamo
e dato che
anche
, quindi
che è diversa da zero. Quindi non si conserva. Notare che non si conserva neppure il modulo della quantità di moto. Supponendo per semplicità
abbiamo
\qed
Cerchiamo adesso di trovare la soluzione dell’Equazione (↓). Si tratta essenzialmente di trovare una funzione proporzionale alla sua derivata seconda. Notiamo che
- La derivata di una funzione esponenziale è proporzionale alla funzione stessa, quindi lo sarà anche la sua derivata seconda:
- La derivata seconda di un seno o di un coseno ha la stessa proprietà:
Tornando all’ Equazione (↓) notiamo però che la costante di proporzionalità deve essere positiva, quindi seno e coseno sono fuori causa. Cerchiamo quindi una soluzione esponenziale. Sostituendo abbiamo
e troviamo due possibili soluzioni:
ma come si verifica facilmente (provate) una qualsiasi combinazione lineare delle due soluzioni è una soluzione. Allora possiamo scrivere
Per determinare le costanti arbitrarie scriviamo
e risolvendo otteniamo
dove abbiamo indicato con
il tratto che sporge inizialmente. In conclusione
Quindi
cresce con una legge praticamente esponenziale nel tempo, fino a quando
. In quel momento tutto il filo si trova sul piano verticale, ed inizia a cadere con accelerazione costante
.
Calcolare dopo quanto tempo
.
(La soluzione apparirà in seguito.)
Calcolare la velocità del filo quando
.
(La soluzione apparirà in seguito.)
Consideriamo adesso la tensione lungo il filo. Introduciamo una coordinata
che ci dice quale punto di quest’ultimo stiamo considerando: in particolare
e
corrisponderanno agli estremi.
Calcolare la tensione
al variare di
. Considerare in particolare il caso
e
.
(La soluzione apparirà in seguito.)
Nel ricavare le Equazioni (↓) e (↓) abbiamo applicato la legge
al tratto di filo sul piano orizzontale e a quello sul piano verticale. Però la massa di questi tratti non è costante nel tempo. \’E legittimo fare questo nel caso considerato? Discuteremo questo punto in dettaglio quando parleremo dei sistemi di massa variabile, ma invitiamo a riflettere prima autonomamente sul problema.