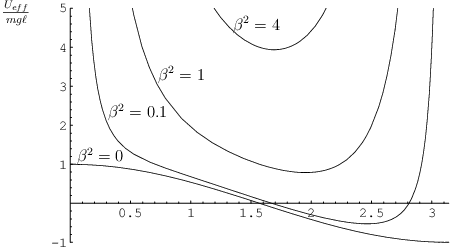Esercitazioni di Fisica 1
Ultima versione: \today
Ancora corpi rigidi e potenziali efficaci
1 Urto di un cilindro contro un gradino

Da quale altezza occorre lasciar cadere un cilindro di massa
e raggio
, affinchè salga sul gradino di altezza
, come in Figura? Si assuma che durante l’arrampicata il punto di contatto cilindro-gradino rimanga fermo.
Chiamiamo
il momento di inerzia del cilindro rispetto al suo centro di massa. Se il cilindro rotola senza strisciare arriva in fondo con energia cinetica
Nell’urto cilindro-gradino si conserva il momento angolare rispetto alla punta del gradino. Il momento angolare immediatamente prima dell’urto vale
e immediatamente dopo
Ponendo
otteniamo il valore di
. Da questo momento si conserva l’energia: per riuscire a salire sullo scalino il centro di massa del corpo deve arrivare sulla verticale del punto di contatto, quindi
Per quale valore di
l’energia dissipata nell’urto con il gradino è minima?
La variazione di energia nell’urto vale
e dato che
vediamo che si deve prendere il massimo valore possibile per
.
Quanto vale
se la massa
- è distribuita uniformemente nel cilindro?
- è tutta distribuita sul bordo?
- si trova tutta sull’asse di rotazione?
Nel primo caso abbiamo
, quindi
. Se la massa è tutta sul bordo
e quindi
. Infine se la massa è tutta sull’asse di rotazione
e quindi
.
La stessa domanda precedente se invece di un cilindro abbiamo una sfera (Lasciato allo studente).
Nel caso del cilindro, è possibile distribuire la massa (anche non mantenendo la simmetria cilindrica) in modo che non venga dissipata energia nell’urto?
Il caso generale si può trattare considerando il centro di massa in una posizione arbitraria, come in figura.
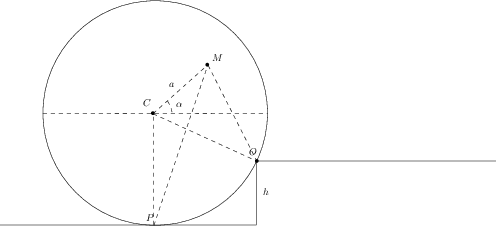
Indicando con
la distanza tra il centro di massa
e il centro del cilindro
e con
l’angolo tra il segmento
e l’orizzontale possiamo scrivere il momento angolare iniziale rispetto a
che si può anche riscrivere utilizzando l’identità
come
Il momento angolare iniziale vale invece
e dall’uguaglianza
troviamo
Per l’energia iniziale abbiamo
e per quella finale
La variazione di energia si scriverà quindi
ed avremo
quando
ossia, svolgendo i calcoli,
D’altra parte
2 YoYo
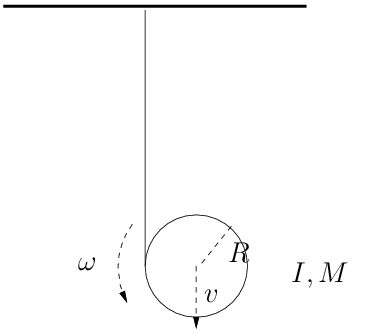
Calcolate l’accelerazione del cilindro in figura, attorno al quale è avvolto un filo inestensibile e privo di massa che si srotola durante la caduta.
Soluzione
Scriviamo le equazioni cardinali. Per il moto verticale del centro di massa abbiamo
e per la rotazione
dove
è il momento di inerzia del cilindro rispetto al suo centro di massa,
. La condizione di rotolamento puro sul filo da
da cui
e sostituendo nella prima equazione si trova
da cui
3 Pendolo sferico
Discutere le traiettorie di un pendolo sferico, cioè di una particella vincolate nello spazio da un filo inestensibile di lunghezza
.
Soluzione
Conviene descrivere il sistema in coordinate sferiche. Possiamo scrivere l’energia cinetica come
e l’energia potenziale
Osserviamo che sulla particella agiscono due forze: la forza peso e la reazione vincolare della superficie. Possiamo scrivere
ma dato che
abbiamo
da cui segue che
. Quindi il momento delle forze non ha componenti verticali e la componente
del momento angolare si conserva:
Utilizziamo questa relazione per riscrivere l’energia totale nella forma
dove
Per comodità abbiamo introdotto la variabile adimensionale
Il grafico qualitativo è riportato in Figura 1↓, per diversi valori di
.